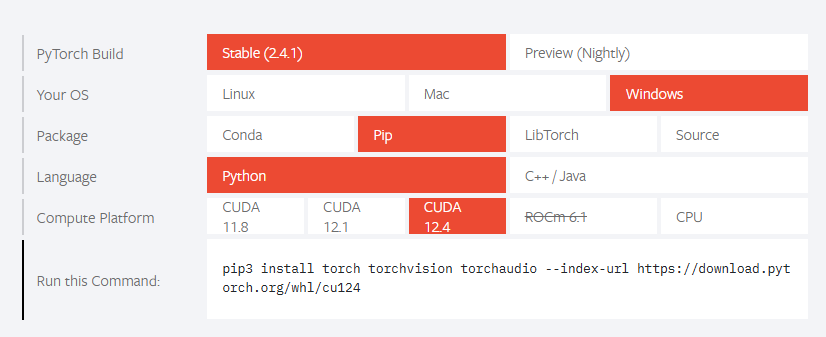
在FastAPI+Vue全栈项目开发中,FastAPI凭借高性能、自动生成接口文档的优势成为后端首选,Vue则以简洁的组件化开发适配前端需求。两者结合部署时,静态文件(Vue打包后的dist资源、后端自身静态文件)的挂载方式 是单容器与多容器部署的核心差异,也是部署过程中静态文件访问404、资源加载失败、页面路由异常等问题的主要诱因。本文将系统梳理FastAPI+Vue全栈项目的部署逻辑,重点拆解单容器与多容器模式下静态文件挂载的核心区别、常见问题及解决方案,同时融入环境变量管控技巧,实现静态文件挂载与接口兼容的联动,助力开发者高效落地全栈项目部署。
一、项目架构与部署前置准备 FastAPI+Vue全栈项目的核心交互逻辑为:前端Vue负责页面渲染与用户交互,后端FastAPI提供接口服务与数据处理,静态文件的加载效率直接决定项目体验。部署前需完成技术栈梳理、项目结构规划及前置准备,为静态文件挂载奠定基础。
1.1 核心技术栈与标准项目结构
后端(FastAPI):核心依赖fastapi、uvicorn、python-dotenv,需配置静态文件挂载及接口管控逻辑,同时处理后端自身静态资源(如图片、配置文件)的访问;
前端(Vue3):核心依赖axios(接口请求)、vue-router(路由管理),打包后生成dist静态文件目录,需配置打包路径适配不同部署场景的静态文件挂载规则;
标准项目结构(适配静态文件挂载,避免路径混乱):
├── backend/ # FastAPI后端目录
1.2 前置依赖安装与静态文件准备 部署前需完成前后端依赖安装和前端打包,确保静态文件可正常用于挂载,同时规避因依赖缺失、打包路径错误导致的部署问题:
1 2 3 4 5 6 7 8 9 10 pip install fastapi uvicorn python-dotenv pip freeze > requirements.txt npm install --registry=https://registry.npmmirror.com npm run build
1.3 核心前置配置:Vue打包路径适配 Vue打包路径(publicPath)是静态文件挂载成功的关键,需根据部署模式(单容器/多容器)配置,否则会导致静态资源加载404:
1 2 3 4 5 6 7 8 module .exports = { publicPath : process.env .VUE_APP_DEPLOY_MODE === 'single' ? '/static/' : '/' , outputDir : 'dist' , assetsDir : 'static' };
可通过前端环境变量区分部署模式,在frontend/.env.single(单容器)和frontend/.env.multi(多容器)中配置:
1 2 3 4 5 6 7 # frontend/.env.single(单容器部署) VUE_APP_DEPLOY_MODE=single VUE_APP_API_BASE=/api # frontend/.env.multi(多容器部署) VUE_APP_DEPLOY_MODE=multi VUE_APP_API_BASE=/api
1.4 辅助配置:环境变量管控接口与静态文件访问 为实现部署的灵活性,可通过环境变量管控接口可用性和静态文件访问权限,避免敏感资源暴露,同时适配不同环境(开发/测试/生产)的部署需求:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 from fastapi import FastAPI, HTTPException, FileResponsefrom fastapi.staticfiles import StaticFilesimport osfrom functools import wrapsfrom dotenv import load_dotenvload_dotenv() app = FastAPI(title="FastAPI+Vue全栈部署实战" ) def enable_by_env (env_var: str , default: bool = False ): def decorator (func ): @wraps(func ) async def wrapper (*args, **kwargs ): is_enabled = os.getenv(env_var, str (default)).lower() == "true" if not is_enabled: raise HTTPException(status_code=404 , detail="接口暂不可用" ) return await func(*args, **kwargs) return wrapper return decorator
二、单容器部署实战(小型项目首选) 单容器部署的核心逻辑:将Vue打包后的dist静态文件与FastAPI后端代码合并,由FastAPI统一负责静态文件挂载和访问 ,最终打包为一个镜像。该模式配置简单、无跨域问题,适合小型项目、演示场景或快速部署需求,核心重点是“静态文件合并复制+FastAPI挂载配置”。
2.1 单容器部署完整配置 2.1.1 项目根目录Dockerfile(静态文件合并挂载核心) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 FROM node:20 -alpine as build-frontendWORKDIR /app/frontend COPY frontend/package*.json ./ RUN npm install --registry=https://registry.npmmirror.com COPY frontend/ . RUN npm run build -- --mode single FROM python:3.11 -slim as build-backendWORKDIR /app/backend RUN apt-get update && apt-get install -y --no-install-recommends gcc && rm -rf /var/lib/apt/lists/* COPY backend/requirements.txt ./ RUN pip install --no-cache-dir -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple COPY backend/ . COPY --from=build-frontend /app/frontend/dist /app/backend/static COPY backend/static /app/backend/static/backend-static FROM python:3.11 -slimWORKDIR /app COPY --from=build-backend /usr/local/lib/python3.11/site-packages /usr/local/lib/python3.11/site-packages COPY --from=build-backend /app/backend /app EXPOSE 8000 ENV PYTHONUNBUFFERED=1 \ ENABLE_HELLO_API=true \ ENABLE_ADMIN_API=false \ STATIC_FILE_ACCESS=true CMD ["uvicorn" , "main:app" , "--host" , "0.0.0.0" , "--port" , "8000" , "--static-dir" , "static" ]
2.1.2 FastAPI静态文件挂载与路由适配(backend/main.py) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 app.mount("/static" , StaticFiles(directory="static" ), name="static" ) @app.get("/api/hello" , summary="测试接口" @enable_by_env("ENABLE_HELLO_API" , default=False async def hello (): return {"message" : "Hello from FastAPI+Vue 单容器部署" } @app.get("/api/admin/panel" , summary="管理员接口" @enable_by_env("ENABLE_ADMIN_API" , default=False async def admin_panel (): return {"data" : {"user" : "admin" , "role" : "super_admin" }} @app.get("/api/health" , summary="健康检查接口" async def health_check (): return {"status" : "ok" , "deploy_mode" : "single-container" } @app.get("/{full_path:path}" async def serve_vue_app (full_path: str ): if not os.getenv("STATIC_FILE_ACCESS" , "true" ).lower() == "true" : raise HTTPException(status_code=403 , detail="静态文件访问被禁止" ) return FileResponse("static/index.html" )
2.2 单容器部署步骤与验证
构建镜像:在项目根目录执行命令,生成单容器镜像:docker build -t fastapi-vue-single:v1.0 .
启动容器:指定环境变量,映射端口(8000端口):
-e ENABLE_HELLO_API=true
验证效果:
访问前端页面:http://localhost:8000,页面正常加载,路由刷新无404;
访问后端接口:http://localhost:8000/api/hello,正常返回响应;
访问静态资源:http://localhost:8000/static/static/logo.png(前端logo),可正常加载。
2.3 单容器部署:静态文件挂载常见问题及解决方案 问题1:Vue路由刷新404 原因:FastAPI默认不处理Vue的SPA路由,刷新非根路径时,FastAPI无法匹配到对应的静态文件;
解决方案:通过@app.get("/{full_path:path}")拦截所有路径请求,转发到Vue入口文件static/index.html,如上述代码所示。
问题2:静态资源(JS/CSS/图片)加载失败 原因1:Vue打包时publicPath配置错误,未指向FastAPI挂载的/static/路径;
解决方案:确认vue.config.js中publicPath为/static/,且打包时指定单容器模式(npm run build -- --mode single)。
原因2:Dockerfile中前端静态文件复制路径错误,未复制到FastAPI可挂载的/app/backend/static目录;
解决方案:核对COPY --from=build-frontend /app/frontend/dist /app/backend/static路径,确保dist目录下的文件直接复制到backend/static目录。
问题3:后端自身静态资源无法访问 原因:后端静态资源未复制到FastAPI挂载的static目录,或访问路径错误;
解决方案:将后端static目录复制到/app/backend/static/backend-static,通过http://localhost:8000/static/backend-static/xxx访问。
三、多容器部署实战(生产环境推荐) 多容器部署的核心逻辑:用两个独立容器分别运行前端(Nginx部署)和后端(FastAPI),静态文件挂载完全独立 ——前端静态文件由Nginx挂载并提供访问服务(Nginx擅长处理静态资源,加载速度更快),后端静态资源由FastAPI自身挂载,通过Docker Compose管理容器通信。该模式前后端解耦,可单独升级、扩缩容,适合中大型项目、生产环境,核心重点是“静态文件独立挂载+Nginx配置+跨容器通信”。
3.1 多容器部署完整配置 3.1.1 后端Dockerfile(backend/Dockerfile,仅挂载后端自身静态资源) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 FROM python:3.11 -slimWORKDIR /app RUN apt-get update && apt-get install -y --no-install-recommends gcc && rm -rf /var/lib/apt/lists/* COPY requirements.txt . RUN pip install --no-cache-dir -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple COPY . . EXPOSE 8000 ENV PYTHONUNBUFFERED=1 \ ENABLE_HELLO_API=true \ ENABLE_ADMIN_API=false CMD ["uvicorn" , "main:app" , "--host" , "0.0.0.0" , "--port" , "8000" , "--static-dir" , "static" ]
3.1.2 前端Dockerfile(frontend/Dockerfile,Nginx挂载前端静态文件) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 FROM node:20 -alpine as build-stageWORKDIR /app COPY package*.json ./ RUN npm install --registry=https://registry.npmmirror.com COPY . . RUN npm run build -- --mode multi FROM nginx:alpine as production-stageCOPY --from=build-stage /app/dist /usr/share/nginx/html COPY nginx.conf /etc/nginx/conf.d/default.conf EXPOSE 80 CMD ["nginx" , "-g" , "daemon off;" ]
3.1.3 Nginx配置(frontend/nginx.conf,静态文件访问核心) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 server { listen 80 ; server_name localhost; location / { root /usr/share/nginx/html; index index.html; try_files $uri $uri / /index.html; } location ~* \.(js|css|png|jpg|gif|ico)$ { root /usr/share/nginx/html; expires 7d ; add_header Cache-Control "public, max-age=604800" ; } location /api/ { proxy_pass http://backend:8000/api/; proxy_set_header Host $host ; proxy_set_header X-Real-IP $remote_addr ; proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for ; } location /backend-static/ { proxy_pass http://backend:8000/static/backend-static/; } }
3.1.4 Docker Compose配置(项目根目录/docker-compose.yml) 核心作用:管理两个容器的构建、启动顺序、网络通信,实现静态文件独立挂载的同时,确保前后端正常交互:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 version: '3.8' services: backend: build: ./backend restart: always environment: - ENABLE_HELLO_API=true - ENABLE_ADMIN_API=false networks: - app-network volumes: - ./backend:/app - ./backend/static:/app/static frontend: build: ./frontend restart: always ports: - "80:80" depends_on: - backend networks: - app-network volumes: - ./frontend/dist:/usr/share/nginx/html networks: app-network: driver: bridge
3.2 多容器部署步骤与验证
构建并启动容器:在项目根目录执行命令,Docker Compose会自动构建镜像并启动两个容器:docker-compose up -d --build
查看容器状态:确认两个容器正常运行,无异常退出:docker-compose ps
验证效果:
访问前端页面:http://localhost(Nginx端口),页面正常加载,路由刷新无404;
访问后端接口:http://localhost/api/hello,Nginx自动转发到后端容器,正常返回响应;
访问前端静态资源:http://localhost/static/logo.png,由Nginx直接返回,加载速度快;
访问后端静态资源:http://localhost/backend-static/xxx,Nginx反向代理到后端容器,正常加载。
3.3 多容器部署:静态文件挂载常见问题及解决方案 问题1:前端静态文件加载失败(404) 原因1:Nginx挂载的前端静态文件路径错误,未找到dist目录;
解决方案:确认前端Dockerfile中COPY --from=build-stage /app/dist /usr/share/nginx/html路径正确,确保dist目录下的文件直接复制到Nginx的默认静态目录。
原因2:Vue打包时publicPath配置错误,未设为/(Nginx根路径);
解决方案:确认vue.config.js中publicPath为/,且打包时指定多容器模式(npm run build -- --mode multi)。
问题2:后端接口请求失败(跨域/转发失败) 原因:Nginx反向代理配置错误,未正确指向后端服务名(Docker Compose中后端服务名为backend);
解决方案:核对Nginx配置中proxy_pass http://backend:8000/api/,确保服务名与Docker Compose中一致,同时配置跨域相关请求头。
问题3:开发环境静态文件热更新失效 原因:未通过volumes挂载本地目录,修改前端/后端代码后需重新构建镜像才能生效;
解决方案:在Docker Compose中添加volumes配置,挂载本地源码/静态文件目录(如上述配置中的volumes节点),修改代码后无需重新构建,容器内文件实时同步。
问题4:静态文件缓存导致版本不兼容 原因:Nginx对静态文件进行缓存,前端升级后,用户浏览器仍加载旧版本静态文件,导致页面显示异常;
解决方案:1. 前端打包时为静态资源添加版本后缀(如app.123456.js),避免缓存冲突;2. Nginx配置静态资源缓存策略,结合版本后缀使用,确保新资源正常加载。
四、单容器与多容器部署:静态文件挂载核心区别(重点) 静态文件挂载的差异是两种部署模式的核心,直接决定部署复杂度、性能和扩展性,以下是详细对比,帮助开发者快速选型:
对比维度
单容器部署(FastAPI统一挂载)
多容器部署(Nginx+FastAPI独立挂载)
静态文件挂载主体
仅FastAPI,负责挂载前端dist和后端自身静态资源
前端由Nginx挂载,后端由FastAPI挂载,各自独立
挂载方式
构建阶段将前端静态文件复制到后端目录,统一挂载
前端dist挂载到Nginx目录,后端静态资源挂载到FastAPI目录,互不干扰
静态文件处理性能
FastAPI不擅长处理静态资源,加载速度一般,高并发下压力大
Nginx擅长处理静态资源,加载速度快,支持缓存优化,性能更优
路由刷新问题处理
通过FastAPI接口拦截,转发到Vue入口文件
通过Nginx的try_files配置,直接处理路由刷新,更高效
跨域问题
无跨域问题(前后端同容器,请求路径一致)
需通过Nginx反向代理解决跨域,配置稍复杂
扩展性
差,前后端耦合,无法单独升级、扩缩容
好,前后端解耦,可单独升级前端/后端,支持水平扩缩容
适用场景
小型项目、演示场景、快速部署,静态资源较少
中大型项目、生产环境,静态资源较多,需优化加载速度
核心问题
Vue路由刷新404、静态资源路径错误、FastAPI服务压力大
Nginx配置错误、跨容器通信失败、静态文件缓存冲突
五、静态文件挂载与接口兼容的联动处理 静态文件挂载的差异可能间接导致“接口看似不兼容”(如静态文件加载失败导致页面无法发起请求、后端静态资源访问权限不足),需结合环境变量管控和挂载配置,实现联动兼容,确保项目稳定运行:
环境变量联动管控:通过环境变量同时管控接口可用性和静态文件访问权限,例如生产环境禁用调试接口的同时,限制后端静态资源的访问,避免敏感信息暴露;
版本同步适配:前端静态文件版本与后端接口版本同步,通过版本标签管理(如v1.0、v2.0),确保挂载的静态文件调用的接口存在且兼容,避免因接口迭代导致的页面异常;
异常兜底处理:前端添加静态文件加载失败的兜底逻辑(如显示默认图片、提示用户刷新),避免因静态文件挂载问题导致页面崩溃;同时在接口拦截器中区分“接口错误”和“静态文件加载错误”,提升用户体验;
权限联动控制:敏感页面(如管理员页面)的静态文件访问,可结合后端接口权限校验,仅登录用户可访问,实现静态文件与接口权限的双重管控。
六、部署实战最佳实践总结
选型原则 :根据项目规模和性能需求选型,小型项目选单容器(快速部署),中大型项目选多容器(性能优、扩展性强);
静态文件配置核心 :单容器重点关注“Vue打包路径+FastAPI挂载+路由转发”,多容器重点关注“Nginx静态文件挂载+反向代理+缓存配置”;
开发效率优化 :开发环境使用Docker Compose的volumes挂载本地目录,实现静态文件和代码热更新,无需频繁构建镜像;
生产环境优化 :多容器部署时,配置Nginx静态资源缓存,提升加载速度;精简容器镜像,降低部署体积;添加容器重启策略,确保服务稳定性;
问题排查技巧 :部署失败时,优先排查静态文件挂载路径、Vue打包配置、Nginx反向代理配置,可通过docker logs查看容器日志,定位问题根源。
七、总结 FastAPI+Vue全栈项目部署的核心难点,本质是静态文件挂载方式的适配 ——单容器部署通过FastAPI统一挂载,追求简单高效;多容器部署通过Nginx与FastAPI独立挂载,追求性能与扩展性。两种模式各有优劣,开发者需根据项目需求灵活选型,重点规避静态文件访问404、路由刷新异常、跨域等常见问题。
本文通过完整的部署配置、代码示例、问题解决方案,详细拆解了两种部署模式的核心逻辑,同时融入环境变量管控技巧,实现静态文件挂载与接口兼容的联动。掌握这些内容后,开发者可快速落地FastAPI+Vue全栈项目的部署工作,无论是小型演示项目还是大型生产项目,都能确保静态文件正常加载、接口稳定通信,提升项目部署效率和运行稳定性。
(注:文档部分内容可能由 AI 生成)